v.11
Metrics are crucial for audio professional applications, tuning the sound of everyday gadgets as mobile phones, or music and audiophile setups. As for everything else whenever traceable knowledge is requested. Making the difference between facts and anecdotal evidence.
Up to E. H. Weber (1795–1878) researchers believed that humans were unable to accurately weight physical quantities. Mr. Weber demonstrated that in fact we are able of quite precise evaluations, not of absolute but of relative quantities. Specifically able to differentiate between nearby sensorial amounts or ratios. What we know in our days as Weber law(s), differential thresholds or just noticeable differences (JNDs). G. T. Fechner (1801–1887) would propose later a logarithmic approach between physical quantities and corresponding sensations, a more elegant and “mathematical” way of representing Weber fractions.
So, when we look at the equation of Loudness, arguably closely related to the perceived sound intensity by humans, everything seems fine
[1] L (dB SPL) = 20 * Log10 Pr/Po
Where
- L is the sound volume or loudness, supposed to correspond to the subjective intensity as perceived by humans
- 20 is a constant K
- Pr is the sound pressure of the actual sound (μPa)
- Po is the reference sound pressure, usually 20 (μPa), supposed to correspond to the absolute threshold of the human ear
And, for further use in this post
- Pd is the sound pressure of the differential or compared sound (μPa) against Pr
Right? No. In fact the relationship between dB as calculated from the above equation and the human auditory perception is problematic, to say the least. And such problematic relationship between dB computations and human perception is not just a problem near the limits, that is close to the absolute threshold (minimum sensed quantity) and to the terminal one (excess of stimulation, saturation); but along all the sensorial scale in-between. That is why wise practitioners do use measures of Db’s because they are expected to but do not rely too much on such evaluations, let it be in the field of audiometry, human factors, industrial safety, etc. Also, seasoned researchers just do not waste time using such Decibel things and instead do use psychoacoustic indicators, inspired by the work of S. S. Stevens (1906–1973). The trade off being that such indicators are based on empirical evidence and computations which are not always clear and straightforward. Meanwhile, engineers in this century as in the last one continue to happily develop hardware and software relying on Db (SPL) computations with a faint relationship with measurable sound perception.
What is wrong with the equation? Yes, there is a ratio, but between the actual sound (Pr) and an absolute threshold one (Po). This is not an acceptable sensorial ratio. In fact such ratio is an oddity with no empirical support. Sensorial ratios have been consistently found but between quantities along the span of sensitivity of a sensory channel. And humans are constantly calibrating their senses to the stimulation available and detectable in their environment (ie, above absolute thresholds and below terminal ones). In fact, there is no need at all to weight an absolute threshold for computing loudness. And then a logarithm of that ratio? Fechner over Weber? Might be mathematically acceptable and a reasonable derivation from the work of Fechner himself, but is nevertheless a non-sense from a experimental psychophysics approach.
Unfortunately most of the quoted research on the basic underpinnings of loudness perception, following a classic approach, is quite dated. And researchers nowadays are so stressed to publish complicated and fancy studies in top journals that they do not have time to re-evaluate simple basic variables. So, let us visit Mr. Weber again. Making a simple experiment, doable with home available tools as the studies of Weber or Jean Piaget (1896-1980); With just a few participants (two, S1 and S2); But nevertheless, in a reasonably well controlled setup.
Figure 1. The audio sample
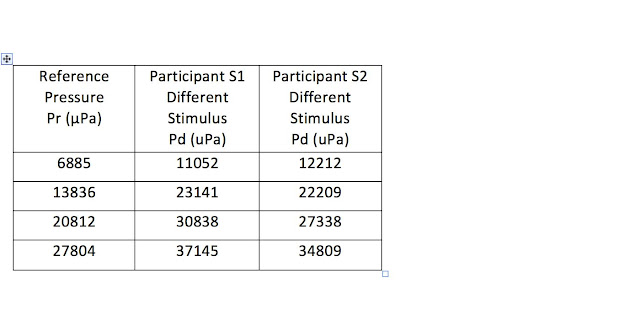
Question: “these 2 (consecutive) sounds are equally loud or one is louder than the other?”. In each trial, one of the four reference sounds (Pd), spanning from 6885 to 27804 μPa (around 51 to 63 dB SPL) was paired with a louder one (Pr). The sequence of pairs of variable sounds loudness (around 3s duration for each consecutive stimulus with a variable interval of 2-5s) was presented to the right ear of each participant by an adapted method of limits, staircase technique, as in audiogram tests. The sounds were of a ticking mechanical pocket watch. Sounds were created and presented with a setup based on Audacity running in a MacBook, an external digital-to-analog converter and amplifier, FiiO Q1 MII, and Sony MDR-7510 headphones. Calibration was done with AudioTools (SPL Pro) running in an iPhone. For the records, even with such simple tools the relationship between volume levels in Audacity and volume levels as measured with AudioTools, from the right channel of the Earphones, was found to be linear and with a correlation of R2=0.99. Sound pressure levels (μPa) were computed from dB (SPL) values following calibration with AudioTools.
Looking at results. What about a simple Weber ratio?
[2] Loudness = Pd/Pr
No, it seems random or more precisely, a disparate inverse relationship among participants.
Plot 1 and 2
And if we use just the difference Pd-Pr, not so weird as a psychophysics measure in some case studies?
[3] Loudness = Pd - Pr
Also not good. A sort of logarithm up to the third value for the first participant, then decreasing. Random/insensitive or linear/increasing to the second participant.
Plot 3 and 4
Then, after several further trials with putative ratios, as a common approach among researchers, to explore empirical data:
[4] Loudness = Pr/Pd
Now it seems to start making sense.
Plot 5 and 6
In sum, perception of Loudness seems to follow a Weber ratio. Providing we are able to find out the good ratios. Audio and acoustics are not a special and magical arena apart from other sensorial domains.
From here, two paths might be suggested.
One, to make further studies on Weberian ratios, refining measures and procedures.
Or, other, more appealing to practical people urging for useful applications, to modify the procedures in search for an updated Fechnerian equation; ie, a new, simpler and more reliable revision of the dB equation, as:
[5] Loudness (dB SPL) = K * Logn Pr (μPa)
For those who might want to play further with the data used here:
Table 1